想必大家都知道初中三角函数包含六种基本函数：正切、余切、正弦、余弦、正割、余割，但是初中三角函数公式容易混淆也同时在考试的时候容易成为一个失分点，所以为了做题目的时候能够正确的运用好三角函数小编特意总结归纳了一些它们其中的一些点一共六个点：

1.锐角三角函数定义

锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec)，余割(csc)都叫做角A的锐角三角函数。

正弦(sin)：对边比斜边，即sinA=a/c

余弦(cos)：邻边比斜边，即cosA=b/c

正切(tan)：对边比邻边，即tanA=a/b

余切(cot)：邻边比对边，即cotA=b/a

正割(sec)：斜边比邻边，即secA=c/b

余割(csc)：斜边比对边，即cscA=c/a

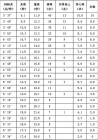
2.特殊角三角函数值

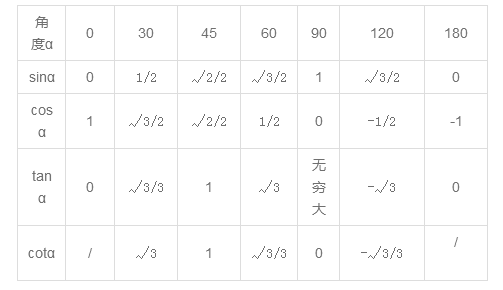
3.三角函数关系

互余角的关系

sin(90°-α)=cosα, cos(90°-α)=sinα,

tan(90°-α)=cotα, cot(90°-α)=tanα.

平方关系

sin^2(α)+cos^2(α)=1

tan^2(α)+1=sec^2(α)

cot^2(α)+1=csc^2(α)

积的关系

sinα=tanα·cosα

cosα=cotα·sinα

tanα=sinα·secα

cotα=cosα·cscα

secα=tanα·cscα

cscα=secα·cotα

倒数关系

tanα·cotα=1

sinα·cscα=1

cosα·secα=1

4.锐角三角函数公式

两角和差公式

sin(A+B) = sinAcosB+cosAsinB

sin(A-B) = sinAcosB-cosAsinB

cos(A+B) = cosAcosB-sinAsinB

cos(A-B) = cosAcosB+sinAsinB

tan(A+B) = (tanA+tanB)/(1-tanAtanB)

tan(A-B) = (tanA-tanB)/(1+tanAtanB)

cot(A+B) = (cotAcotB-1)/(cotB+cotA)

cot(A-B) = (cotAcotB+1)/(cotB-cotA)

三角和的公式

sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγ

cos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγ

tan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)

倍角公式

tan2A = 2tanA/(1-tan² A)

Sin2A=2SinA•CosA

Cos2A = Cos^2 A--Sin² A =2Cos² A-1 =1-2sin^2 A

三倍角公式

sin3A = 3sinA-4(sinA)³;

cos3A = 4(cosA)³ -3cosA

tan3a = tan a • tan(π/3+a)• tan(π/3-a)

半角公式

sin(α/2)=±√((1-cosα)/2)

cos(α/2)=±√((1+cosα)/2)

tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα

积化和差公式

sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]

cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]

cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]

sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]

和差化积公式

sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]

sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]

cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]

cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]

万能公式

sin(a) = [2tan(a/2)] / {1+[tan(a/2)]²}

cos(a) = {1-[tan(a/2)]^2} / {1+[tan(a/2)]²}

tan(a) = [2tan(a/2)]/{1-[tan(a/2)]^2}

推导公式

tanα+cotα=2/sin2α

tanα-cotα=-2cot2α

1+cos2α=2cos^2α

1-cos2α=2sin^2α

1+sinα=(sinα/2+cosα/2)^2

5.三角形面积定理

6.三角函数的图象性质

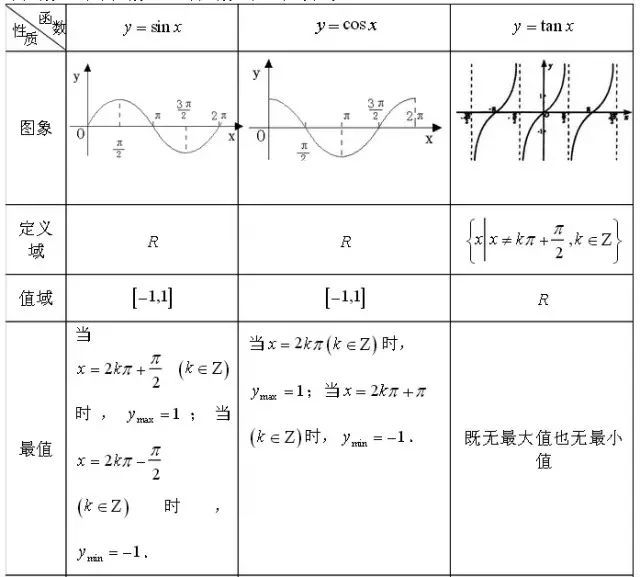
综上所述，初中三角函数的六个点的已经一一列举完毕，希望能帮助同学们能够熟练掌握这一部分知识了，以后做题的时候能够正确运用其中的公司不再产生混淆。